Number System Questions Practice Question and Answer
8 Q: When 1062, 1134 and 1182 are divided by the greatest number .x, the remainder in each case is y. What is the value of (x − y)?
1040 064ba4fa5c3da05b2213e134d
64ba4fa5c3da05b2213e134d- 117false
- 218true
- 316false
- 419false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 2. "18"
Explanation :


The value of (x-y) will be 18
Q: The east positive integer that should be subtracted from 3011 x 3012 so that the difference is a perfect square is-
1038 0630351bd29cb4630442475e5
630351bd29cb4630442475e5- 13009false
- 23010false
- 33011true
- 43012false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 3. "3011"
Explanation :
We know that 3011 x 3012
= 3011 (3011 + 1)
= (3011)2 + 3011
We know
Required least number = 3011
Q: 64329 is divided by a certain number. While dividing, the numbers, 175, 114 and 213 appear as three successive remainders. The divisor is?
1036 06220c43360ee9a48009afe5b
6220c43360ee9a48009afe5b- 1184false
- 2224false
- 3234true
- 4296false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 3. "234 "
Explanation :
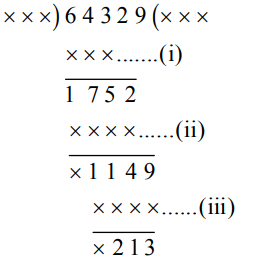
Number at (i) = 643 – 175 = 468
Number at (ii) = 1752 – 114 = 1638
Number at (iii) = 1149 – 213 = 936
Clearly, 468, 1638 and 936 are multiples of 234 and 234 > 213.
Divisor = 234
Q: Amit ranked 7th from the top and 26th from the bottom in his class. How many students are there in the class?
1036 064996a8ccae316dfef834ceb
64996a8ccae316dfef834ceb- 131false
- 233false
- 327false
- 432true
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 4. "32"
Q: In a class, there are ' z ' students. Out of them ‘x’ are boys. What part of the class is composed of girls?
1033 05ee84aec79b5ea388bec1435
5ee84aec79b5ea388bec1435- 1$$1-{x\over z} $$true
- 2$${x\over z}-1 $$false
- 3$${x\over z} $$false
- 4$${z\over x} $$false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "$$1-{x\over z} $$"
Q: The second number in the given number-pairs is obtained by performing certain mathematical operation(s) on the first number. The same operation(s) are followed in all the number-pairs EXCEPT one. Find that odd number-pair.
1023 0644aa3e0244f7ecdff5ceed8
644aa3e0244f7ecdff5ceed8- 1169 : 14true
- 2225 : 18false
- 3196 : 17false
- 4256 : 19false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 1. "169 : 14 "
Q: When (6767 +67) is divided by 68, the remainder is-
1022 06303364629cb46304423ee34
6303364629cb46304423ee34- 113false
- 263false
- 366true
- 467false
- Show AnswerHide Answer
- Workspace
- SingleChoice
Answer : 3. "66"
Explanation :
(6767+ 67) = 67(6766 + 166)
As 66 is an even number
We know 6766 is an even number
We know (6766 + 1) is perfectly divisible by (67 + 1)
i.e. 68
We know The remainder = 66
(6767+ 67) = 67(6766 + 166)
Q: A four digit number is formed by writing a two digit number together twice like: 15:15, -3737 etc. A number of this form will be exactly divisible by which of the following numbers
1012 063228838cb090a254fcd9b05
63228838cb090a254fcd9b05- 1125false
- 2101false
- 3123true
- 4147false
- Show AnswerHide Answer
- Workspace
- SingleChoice

