A Cistern can be filled by a tap in 4 hours while it can be emptied by another tap in 9 hours. If both the taps are opened simultaneously then after how much time will the cistern get filled?

One-fourth of a tank holds135 litres of water. What part of the tank is full if contains 180 litres of water?

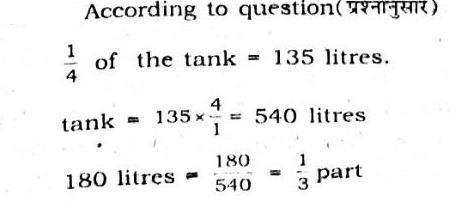
Two pipes, A and B, can fill a tank in X minutes and 6 minutes, respectively. If both the pipes are used together, then they take 1.5 minute to fill the tank. Find the value of X.

A cistern has 3 pipes A, B and C. A and B can fill it in 3 and 4 hours respectively, and C can empty it in 1 hour. If the pipes are opened at 3 p.m., 4 p.m. and 5 p.m. respectively on the same day, the cistern will be empty at-

One filling pipe P is three times faster than another filling pipe Q, if P can fill tank in 24 hours, then what is the time taken to completely fill the tank if both the pipes are opened together?

A pipe can fill a tank in x hours and an another can empty it in y hours. In how many hours will they together fill it. If y>x?

Pipes A and B together can fill a tank in 16 hours, whereas pipe C alone can empty the full tank in 24 hours. A and B were opened together for 10 hours and then closed. Pipe C was then opened. The tank will now be emptied by C in:

Two pipe A and B can fill a tank in 16 hrs and 12 hrs respectively. The capacity of the tank is 240 litres. Both the pipes are opened simultaneously and closed after 2 hrs. How much more water (In Liters) needed to fill the tank?