Clock Reasoning Formula with Examples for SSC and Bank Exams

Many students don't know how to use clock reasoning formulas to solve clock reasoning questions in the competitive exams. In this blog, you can learn the correct use of clock reasoning formulas with examples to solve clock related problems quickly in SSC and bank exams.

Here I am sharing some important clock reasoning formula with examples, these formulas help you to solve clock based questions accurately. Let's learn important fact and formulas to solve clock reasoning problems. 

Try to solve clock reasoning problems your self after learning properly clock problems formula and tricks in English by visit here. You can learn in Hindi by click on clock reasoning trick and formula in Hindi for better practice of this topic. 

Clock Reasoning Formula with Examples:

Important facts and Formulas 

A clock has 12 equal divisions, which are known as hours. Angle covered in 12 divisions (hours) = 360⁰ .So the angle covered in $$1 \ hours = {360^0 \over 12}=30^0$$

Thus, each needle of a clock covers the angle of 30⁰ to go from one division to the next, but it takes different times to cover this distance.

Hour Needle:

It make an angle of 30⁰ in 60 minutes. So, in 1 minute, it will make an angle of $${30^0\over60^0}={1^0\over2}$$

Minute Needle :

It makes an angle of 30⁰ in 5 minutes. So, in 1 minute, it will make an angle of $${30^0\over5}=6^0$$

Second Needle:

It makes an angle of 360⁰ in 60 second. So, in 1 second, it will make an angle of $${30^0\over60}=6^0$$

Distance covered by hour needle & minute needle in 1 minute: 

A minute needle covers the distance of 60 minutes in 60 minute, whereas an hour needle covers the distance of 5 minutes in 60 minutes. Thus, the minute needle covers 55 minutes’ more distance in 60 minute than the hour needle.

∴ it covers the distance of 55 minute in 60 minutes.

Thus, it will cover the distance of 1 minute in 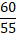 min. OR  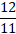min.

Important Clock Reasoning Formula with Examples:

Ex.1. It is 4 hrs. 40 min in a clock. Find the angle between both the needles of a clock.

(A) 100⁰               

 (B) 80⁰                    

(C) 120⁰               

(D) 200⁰

Explanation:

1 Division = 30⁰

So, 4 Division = 30 × 4 = 120⁰

But, the hours needle has already covered the distance of 40 min. from its side, so the angle covered in these 40 min. $$={1\over2}×40=20^0 $$

Now, the angle covered between both needles = 120⁰ – 20⁰ = 100⁰

Second Method:

To find the angle   $$={11×min-60×time\ given\over2}$$$$= {11×40-60×4\over2}$$$$= {200\over2}=100^0$$

Ex.2. What will be the angle formed between needles of a clock at 8 hrs.20 min. ?

(A)   130⁰                       

(B) 140⁰                        

 (C)  120⁰                        

(D) 70⁰

Explanation:

Total divisions between both needles = 4

So, angle = 4×30=120⁰

But, the hour needle has already covered the distance of 20 min. So, the angle covered by the hours needle in 20 min.

$$={1\over2}×20^0=10^0$$

Thus, the angle formed between both needles = 120 + 10 = 130⁰

Second Method:

To find the angle   $$={11×min-60×time\ given\over2}$$$$= {11×20-60×8\over2}$$$$= {200-480\over2}={260\over2}=130^0$$

Ex.3. The mirror image of a clock shows 11.20 hours time. Find the actual time in the clock.

(A) 12.10             

 (B) 1.40                

 (C) 12.40              

(D) 6.30

Explanation:

Actual time = 23.60 – 11.20 = 12.40

Note – It is convenient to deduct the given time from 11.60 if the given time is before 11.00, but if it is later than 11.00, then it is deducted from 23.60.

Ex.4. It is 2.40 hours in a clock. What will be the angle between both needles of a clock ?

(A) 180⁰                 

(B) 160⁰                 

(C) 320⁰                

(D) None of these.

Explanation:

To find the angle =   $$={11×min-60×time\ given\over2}$$

$$= {11×40-60×2\over2} $$ 

$$={440-120\over2}$$$$={320\over2}=160^0$$

Ex.5. It is 5.10 hours in a clock. What will be the angle between the hour needle & the minute needle of that clock?

(A) 265⁰               

 (B) 80⁰                    

 (C) 85⁰                  

(D) 105⁰

Explanation:

 $$={11×min-60×time\ given\over2}$$$$= {11×10-60×5\over2}$$

 $$= {110-300\over2}={190\over2}=95^0$$$$⇒360^0-95^0=265^0$$

Keep practice clock reasoning formula with examples and ask me in the comment section if you face any problems