Compound Interest Formula with Example for SSC and Bank Exams

Students should learn properly the use of compound interest formula with examples for SSC and bank exams. Because compound interest questions asked often in competitive exams. These compound interest formulas are not difficult to use. You just need to learn or practice of using compound interest formulas with examples.
So here you can learn or practice, how to use compound interest formula in differential equations or questions with examples. You can practice also of compound interest questions and answers to bright your performance level.
Know about Problems on Simple Interest and Compound Interest and increase your mental ability.
Compound Interest Formula with Example for Competitive Exams
Interest
When a person (borrower) takes money (loan) from another person or a bank (lender,) then the first person pays some money to another person (lender) for the use of money lent. This extra money paid to the lander is known as interest.
Compound Interest (C.I)
While calculation compound interest, the simple interest which is calculated for the principle of first year, is added to the principal. The result of this addition becomes the principle calculated for second year and this interest is again added to the principle used for the second year. This new addition works as a principal for the third year and this process keeps going on for the stipulated time. Finally, the original principal is subtracted from the last year’s amount.
The result of this subtraction is called compound interest.
Important Facts and Formula
Let, Principal = P, Rate = R% per annum and Time = n yr
1. If interest is compounded annually, then
$$ Amount\ = P \left(1+{R\over100}\right)^n $$
$$ Compound \ = P\left( {\left(1+{R\over100}\right)^n }-1\right)$$
Or CI = Amount-Principal
2. When interest is compounded Half-yearly:
$$ Amount\ = P \left(1+{(R/2)\over100}\right)^ {2n} $$
3. When interest is compounded Quarterly:
$$ Amount\ = P \left(1+{(R/4)\over100}\right)^ {4n} $$
4. When interest is compounded Annually but time is in fraction, say ![]() Years.
Years.
$$ Amount\ = P \left(1+{R\over100}\right)^ 3 × \left(1+{{2\over5}R\over100}\right) $$
5.When Rates are different for different years, say, R1%, R2%, R3%, for 1st, 2nd and 3rd year respectively.
$$Then, Amount = P \left(1+{R_{1}\over100}\right)\left(1+{R_{2}\over100}\right)\left(1+{R_{3}\over100}\right)$$
6. Present worth of Rs. x due n years hence is given by :
$$Present \ worth={x\over\left( 1+{R\over100}\right)^n}$$
Ex.1.Find compound interest of Rs. 7500 at 4% per annum for 2 years, compounded annually.
Solution
$$ Amount \ = Rs\left(7500× {\left(1+{4\over100}\right)^2}\right)=Rs \left(7500× {26\over25}×{26\over25}= Rs.8112\right)$$
∴ C.I = Rs. (8112 – 7500)= Rs. 612.
Ex.2.Find compound interest on Rs.8000 at 15% per annum for 2 years 4 months, compounded annually.
Solution
Time = 2 years 4 month = 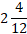 years =
years = 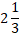 years.
years.
$$ Amount \ = Rs\left(8000× {\left(1+{15\over100}\right)^2}×{\left({1}+{{{1\over3}×15}\over100}\right)}\right)$$
$$=Rs \left(8000× {23\over20}×{23\over20}×{21\over20} =Rs.11109.\right)$$
∴ C.I = Rs. (11109 – 8000)= Rs. 3109.
Ex.3.Find the compound interest on Rs. 10,000 in years at 4% per annum, the interest being compounded half-yearly
Solution
$$ Amount \ = Rs\left(10000× {\left(1+{2\over100}\right)^4}\right)$$
$$=Rs \left(10000× {51\over50}×{51\over50}×{51\over50}×{51\over50}\right) =Rs.10824.32.$$
C.I= Rs. (10824.32-10000)=Rs.824.32
Ex.4.Find the compound interest on Rs. 16,000 at 20% per annum for 9 months, compound quarterly.
Solution
Principal = Rs. 16000; Time = 9 month = 3 quarters;
Rate = 20% per annum = 5% per quarter.
$$∴ Amount\ = Rs\left(16000 ×{\left(1+{5\over100}\right)^3 }\right)$$
$$=\left(16000× {21\over20}×{21\over20}×{21\over20}\right)=Rs.18522$$
∴ C.I= Rs. (18522-16000)=Rs 2522.
Ex.5. If the simple interest on a sum of money at 5% per annum for 3 year is Rs.1200, find the compound interest on the same sum for the same period at the same rate.
Solution
Clearly, Rate= 5% p.a, Time= 3 years, S.I = Rs. 1200
$$So, Principal = \ Rs\left({100×1200\over3×5}\right) $$
$$∴ Amount\ = Rs\left(8000 ×{\left(1+{5\over100}\right)^3 }\right)$$
$$=\left(8000× {21\over20}×{21\over20}×{21\over20}\right)=Rs.9261$$
I hope these important compound interest formula with examples will helpful for your competitive exams. Keep practice with compound interest questions in hindi and get better rank in competitive exam.
Ask me in the comment section anything related compound interest formula with examples if you have any problems or doubt.



