Cube Problems with Solutions for SSC and Bank Exams
Cube is an important topic in the competitive exams because every year asked questions from this topic. Here are the explained different cube problems with solutions from which practices, you can easily solve these type of questions in the competitive exams.
So, continue your practice by given these some cube problems with solutions which will help you to improve your score in the competitive exams. Click here to solve Square Root and Cube Root Problems with Solutions.
Cube Problems and Solutions for Competitive Exams
What is Cube?
A cube is a three-dimensional solid having 6 faces, 12 edges and 8 corners. All the edges of a cubes are equal and hence all the faces are square in shape.
The questions on cubes may belong to anyone of the following categories:
1. A cube is cut by making certain specified number of cuts. The directions in which the cuts are made may or may not be given. We are to find the number of identical pieces resulting out of the given cut.
2. The number of identical pieces, into which a cube is cut, is given and we need to find the number of cuts.
3. A cube could be painted on all or some of its faces with the same colour or different colours and then cut into a certain specified number of identical pieces. The questions of the form- "How many small cubes have 2 faces painted?" "How many smaller cubes have only one face painted?" etc. could then be framed.
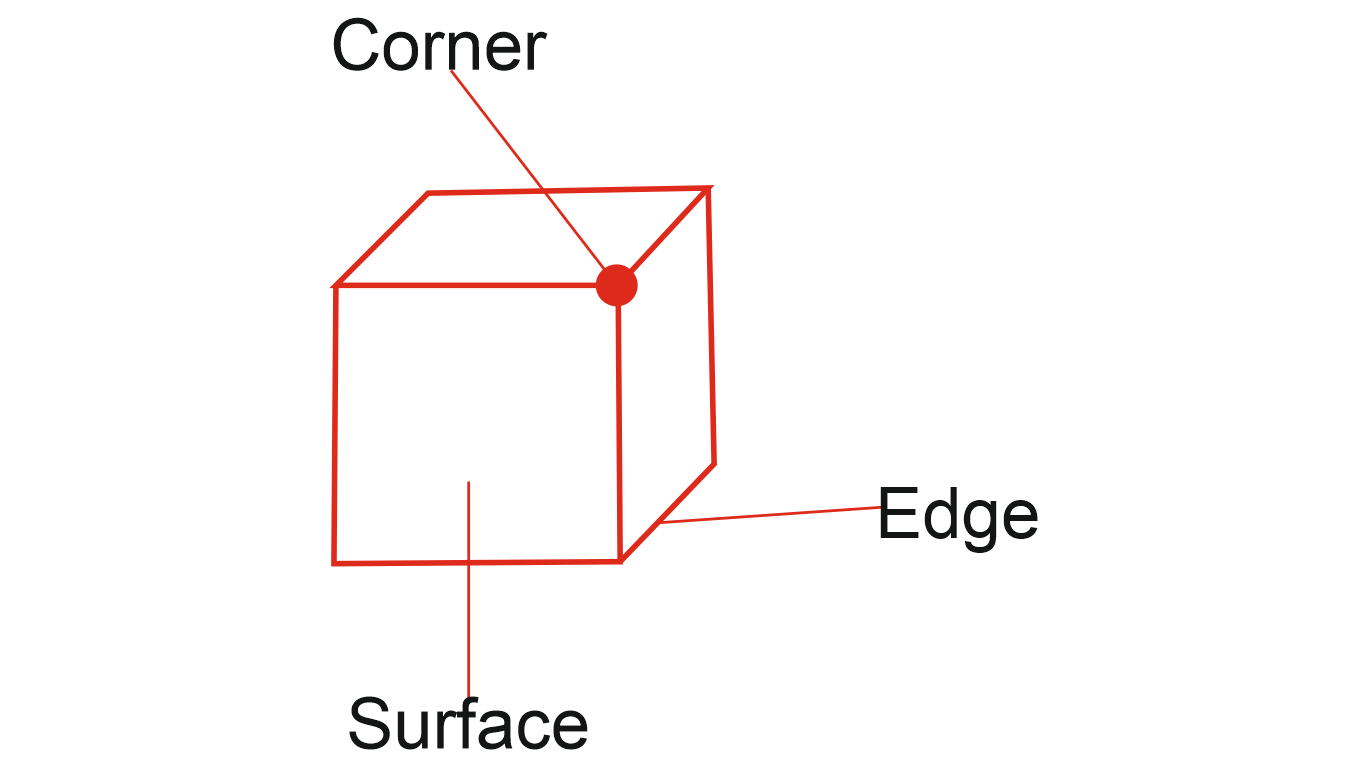
To solve the questions related to cubes you should definitely follow the given rules. The given rules help you to memories the shortcuts useful in solving the questions.
lf a cube is painted on all six surfaces and cut into x number of identical cubes then, $$ n=\ ^3\sqrt {x } \ $$
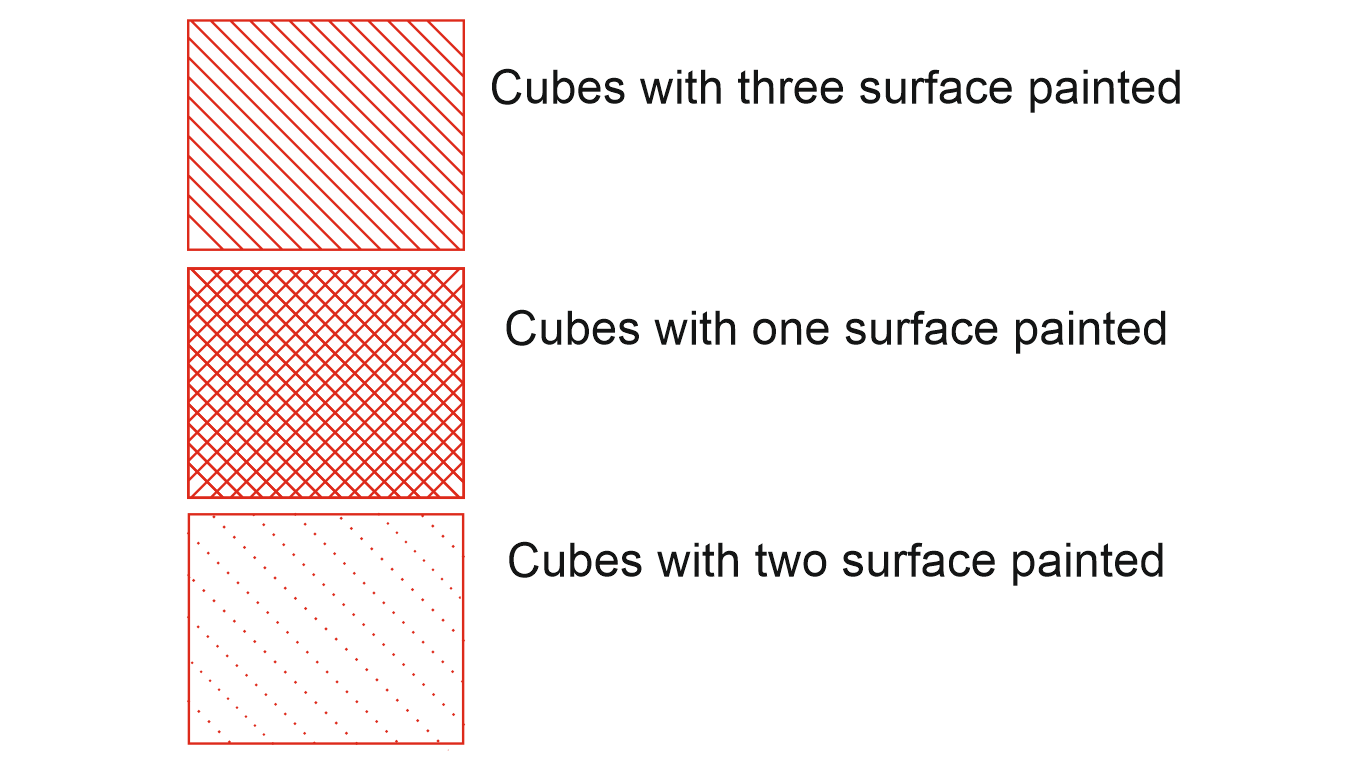
1. Number of cubes having no surface pointed = (n - 2)3
2. Number of cubes having one surface painted (n - 2)2 x 6
3. Number of cubes having two surfaces painted (n- 2) x 12.
4. Number of cubes having three surfaces painted = 8
5. There cannot be a cube which has more than three surfaces painted.
Note : - If a cube of side ‘a’ cm is cut into pieces such that each side of the smaller cube is of “b” cm then $$ n= \left({a\over b}\right)^3$$
Q.1. A cube is cut into two equal parts along a plane parallel to one of its faces. One piece is then coloured red on the two larger faces and green on the remaining while the other is coloured green on two smaller adjacent faces and red on the remaining. Each is then cut into 32 cubes of the same size. The 64 cubes are then mixed up.
1. How many cubes have no coloured face at all?
(A) 16
(B) 8
(C) 4
(D) 0
Ans . D
In both the stacks, there is no cube which has no coloured face at all.
Q.2. How many cube have only one coloured face?
(A) 8
(B) 16
(C) 20
(D) 24
Ans . D
Four cubes (in columns a3, a4, a5 and a6) in each of the two layers A2 and A3 in stack A and similarly four cubes (in columns b3, b4, b5 and b6) in each of the two layers B2 and B3 in stack B have only one coloured face.
Thus, there are (4 x 2)+(4 x 2) = 8+8 16 such cubes.
Q.3. How many cubes have two red and one green face?
(A) 4
(B) 8
(C) 12
(D) 16
Ans . A
There is no cube in stack A which has two red faces. Two cubes (in columns b7 and b8) in layer B1 and two cubes (in columns b1and b2) in layer B4 in stack B have two red and one green face.
Thus, there are (2 + 2)= 4 such cubes
Q.4. How many cubes have one face red another green?
(A) 32
(B) 24
(C) 16
(D) 8
Ans . B
Four cubes (in columns a3, a4, a5 and a6) in each of the two layers A1 and A4 and four cubes (in columns a1, a2, a7 and a8) in each of the two layers A3 and A4 in stack A have one face red and another face green.
Four cubes (in columns b3, b4, b5 and b6) in layer B1, and two cubes (in columns b1 and b2) in each of the two layers B2 and B3 in stack B have one face red and another face green. Thus, there are (4 x 2) + (4 x 2)+ 4+ (2 x 2) = 8+ 8+4+4 24 such cubes.
Q.5. What is the number of cubes with at least one green face?
(A) 46
(B) 38
(C) 36
(D) 28
Ans . B
Eight cubes (in columns a1, a2, a3, a4, a5, a6, a7 and a8) in each of the two layers A1 and A4 and four cubes (in columns a1, a2, a7, and a8) in each of the two layers A2 and A3 in stack A have at least one green face.
Eight cubes (in columns b1, b2, b3, b4, b5, b6, b7, b8) in layer B1 and two cubes (in columns b1 and b2) in each of the three layers B2, B3 and B4 in stack B have at least one green face.
Thus, there are (8 x 2)+(4 x 2)+8 (23) = 16+8+8+6 = 38 such cubes.
If you want to ask anything related cube problems and its solutions, you can ask me in the comment section. Visit on the next page for more practice.
Showing page 1 of 2
enhttps://www.examsbook.com/cube-problems-with-solutions21cube-problems-with-solutionsAbout author
Vikram Singh
Providing knowledgable questions of Reasoning and Aptitude for the competitive exams.
Read more articles