Cube Root and Square Root Formula for Competitive Exams

Cube root and square root is a topic of quantitative aptitude which questions are frequently asked in the competitive exams. If you are preparing for SSC, Banking or any other competitive exam, so here given cube root and square root formulas will be very useful for your preparation. 

In this blog, you will get examples of cube root and square root and their solutions also as well as formulas. These examples, solutions, and formulas will help you to understand this topic easily. 

Practice more with Square Root and Cube Root Problems with Solutions to obtain good marks in the competitive exams.

Formula and Methods of Square and Cube Root

Definition of Cube

If a number is multiple two with itself, then the result of this multiplication is called the cube of that number. E.g., cube of 6 = 6 × 6 × 6 = 216.

Definition of Cube Root 

The cube root is that number the cube of which itself gives the given number. The cube root is denoted by the symbol ‘³√’. E.g., $$ \ ^3\sqrt {8}=^3\sqrt {2 ×2 ×2} = 2$$

To find cube root we use the following method.

Prime Factorisation Method 

This method has the following steps

Step I Express the given number as the product of prime factors.

Step II Keep these factors in a group of three.

Step III Take the product of these prime factors picking one out of every group ( group of three) of the same primes. This product gives us the cube root of given number.

Ex. Find the cube root of 9261.

(A) 22

(B) 21

(C) 23

(D) 24

Solution

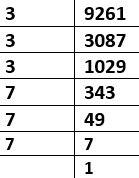
Prime factors of 9261

= (3×3×3)×(7×7×7)

$$ ^3\sqrt {9261 }= \ ^3\sqrt {3×3×3×7×7×7 } \  $$

Now, taking one number from each group of three, we get

   $$ ^3\sqrt {9261 } = 3×7 = 21$$

Important Trick

To find the cube of any number for two places after decimal

Let the given number be x, then take a number y in such a way that y should be near x and is a perfect cube.

$$ ^3\sqrt {x } = {2y+x\over3×y^{2/3}} $$

  $$ ^3\sqrt {66 }=? Here, x=66, y = 64=4^3$$

  $$ Now, \ ^3\sqrt {66 }={2×64+66\over3×(64)^{2/3}}$$

   $${128+66\over3×16}={194\over48} = 4.04 \ (approx)$$

Definition of Square 

If a number is multiplied with itself, then the result of this multiplication is called the square of that number. E.g, square of 6 = 6 × 6 = 36.

Definition of Square Root

The square root of a number is the number is the number, the square of which is equal to the given number. It is denoted by symbol ‘√’ called the radical sign. E.g., $$ \sqrt {81 } \ =\sqrt {9×9 }=9 \ $$

To find the square root we use the following methods

Prime Factorisation Method 

This method has the following steps

Step I Express the given number as the product of prime factors.

Step II Keep these factors in pairs.

Step III Take the product of these prime factors taking one out of every pair of the same primes. This product gives us the square root of the given number.

Ex. Find the square root of 1089.

(A) 34

(B) 33

(C) 32

(D) 22

Solution 

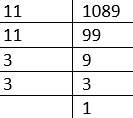
Prime number of 1089 = 11×11×3×3

$$ →\sqrt {1089 } \ = \sqrt { 11×11×3×3} \ = 11×3=33$$

Division Method of Square

We can use the following steps 

Step I In given number, mark of the digit in pairs (also called period) starting from the unit’s digit.

Step II Divide the pair or period of the left side by a number whose square is equal to or less than that period. Write this number at the place of divisor and quotient and find the remainder.

Step III Bring down the next period and write to the left of remainder.

Step IV Write the double of quotient at the place of divisor. Now, write a digit to the right side of divisor which gives the products when multiplying with divisor, equal to or less than dividend.

Step V Write this digit is quotient also find the remainder.

Step VI Repeat the whole process till there is no period left over to be brought down. Thus, the quotient obtained will be the required square root of given number.

Important Tips for Division

1. Division method should be applied, when the given number is, so large that it is very difficult to find its square root by the prime factorisation method.

2. We can make a number which is not a perfect square, a perfect square by multiplying or dividing the number by those factors of it which are not contained in pairs.

3. A perfect square can never end with 

● An odd number or zeroes.

● 2, 3, 7 and 8.

4. If in a number, number of digits is even (say k), then number of digits in its square root will be k/2 and if the number of digits is odd (say k), then the number of digits in its square root will be (k+1/2).

Example.  What is the square root of 151321?

(A) 386

(B) 384

(C) 389

(D) 400

Solution

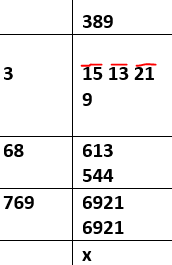
⸫ Required square root = 389

Important Trick

To find the square root of any number for two places after decimal. Now, break the given number (say) x in two part (say) y and z such that one part (say) y is a perfect square, then 

  $$ \sqrt {x } \ = \sqrt {y\pm z} \ = \sqrt {y\pm \ {z\over2\sqrt { y} \ } } $$

  $$ e.g., \sqrt { 156} =\sqrt {144+2 }=\sqrt {144 }+{12\over2\sqrt { 144} \ } \  \ \  $$

  $$ =12+{12\over2×12}=12.5 (approx.) $$

How to calculate the Square Root of Decimal Numbers ?

If in a given decimal number, the number of digital after decimal are not even, then we put a 0 at the extreme right.

Now we mark off the periods and try to calculate the square root applying the division method mentioned above.

Ex. Find the square root of 147.1369.

(A) 12.15

(B) 14.11

(C) 12.13

(D) 11.12

Solution

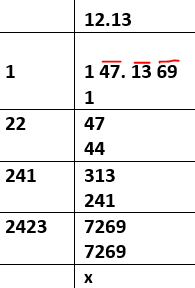
⸫ Required square root = 12.13

Examples with solutions:

Q.1. Find the cube root of 2744

(A) 14

(B) 18

(C) 16

(D) 22

Solution.  

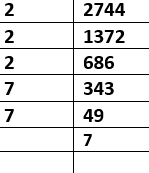
Resolve the given number as the product of prime factors and take the product of prime factors, choosing one out of three of the same prime factors. Resolving 2744 as the product of prime factors, we get:

2744 = 2³×7³

$$ =\ ^3\sqrt {2744}=2×7=14 \ $$

Q.2. By what least number 4320 be multiplied to obtain a number which is a perfect cube?

(A) 40

(B) 30

(C) 20

(D) 50

To make it a perfect cube, it must be multiplied by 2×5² = i.e. 50

Q.3. If the number p is 5 more than q and he sum of the squares of p and q is 55, then the product of p and q is 

(A) 10

(B) – 10

(C) 15

(D) – 15

p-q = 5

p²+q²= 55

On squaring both sides in Eq. (i), we get

(p-q)² = 5²

→ p²+q² – 2pq = 25 → 55 – 2pq = 25

→ – 2pq =  - 30

⸫ pq = 15.

Q.4.The value of $$ \sqrt { - \sqrt {3 }+\sqrt {3+8\sqrt { 7+4\sqrt { 3} \ } \  } \  \ } \   $$ is 

(A) 3

(B) 4

(C) 1

(D) 2

$$ =\sqrt { -\sqrt {3 } \ +\sqrt {3+8(2+\sqrt { 3} \ ) } \ } \ $$

  $$ =\sqrt {-\sqrt { 3} \ +4+\sqrt { 3} \  } \ $$

  $$ =\sqrt { 4} \ = 2 $$

Q.5. Each student of class X contributed some money for a picnic. The money contributed by each student was equal to the cube of the total number of students. If the total collected amount was Rs. 29791, then find the total number of students.

(A) 15

(B) 27

(C) 31

(D) 34

⸫ Total number of students

$$ =\ ^3\sqrt {29791}= \ ^3\sqrt {31×31×31} $$