Decimal fraction formula with examples for ssc and bank Exams

Decimal fractions questions definitely asked in competitive exams. Decimal fraction questions are very important questions. But students face difficulty during solve decimal fraction questions because they make mistakes in using decimal fraction formula.
Here in this article, you can learn to use decimal fraction formula with examples and improve your performance as well. After learning the correct use of decimal fraction formula you can practice also of decimal fraction questions and answers of aptitude.
You should know the complete detail of decimal fraction with its types.
Decimal fraction formula for with examples for Competitive Exams
Definition of a fraction: A number of the form of ![]() , where Y
, where Y ![]() o, is known as the fraction. Here, x and y are respectively known as the numerator and denominator of the fraction.
o, is known as the fraction. Here, x and y are respectively known as the numerator and denominator of the fraction.
Again, a fraction is a rational number too.
Thus, Fraction = $$ = {Numerator \over Denominator}= {N \over D} $$
Definition of Decimal fractions: The fraction, in which denominators has the powers of 10 are called decimal fraction. e.g, 10th part of unit = ![]() for converting a decimal fraction into a simple fraction, place 1 in the denominator under the decimal point. Then, after removing the decimal point, places as many zeroes after it as the number of digits after the decimal point. Now, reduce the fraction in its smaller form.
for converting a decimal fraction into a simple fraction, place 1 in the denominator under the decimal point. Then, after removing the decimal point, places as many zeroes after it as the number of digits after the decimal point. Now, reduce the fraction in its smaller form.
Eg. 5.76 = ![]() =
= ![]()
Addition and Subtraction of Decimal Fraction
For addition or subtraction of decimal fraction, write the decimal in such a way that all the decimal points are in the align form, then these numbers can add or subtract in a simple manner.
Ex. 353.5+2.32+43.23 is equal to
(A) 400.00
(B) 398.5
(C) 399.5
(D) 375.9
Solution:
353.50
2.32
+43.23
-------------
399.05
-------------
Multiplication of Two or more Decimal Fraction
For multiplication of two or more decimal fractions, multiply then without considering the decimal points and then in the product, decimal point is maked as many places of decimal as the sum of the numbers of decimal places in the given numbers.
Ex. 4.3 × 0.13 is equal to
(A) 0.599
(B) 0.622
(C) 5.99
(D) None of these
Solution:
43 × 13 = 599
Sum of the decimal places = (1+2) = 3
![]() Required product = 0.599
Required product = 0.599
Dividing a Decimal Fraction by an integer
If we divide a decimal number b an integer, then at first divide the number ignoring the decimal point and last put the decimal after the number of digits (from right) according at in the given number.
Ex. Divide 0.81 by 9 is equal to
(A)0.9
(B)0.09
(C) 9
(D) None of these
Solution:
$$ {81 \over 9}=9→{0.81 \over 9}=0.09 (Two\ Place\ of \ Decimal) $$
If we divide the decimal number by multiple of 10, then we move the decimal point to the left by the respective number of zeroes eg.![]()
Division of Decimal Fractions
If divisor and dividend both are decimal numbers, then first convert them into the simple fraction by putting numbers of zeroes in the denominators of both. Now divide them.
Ex. Divide 0.4 by 0.007 is equal to
(A) 600
(B) 60
(C) 6000
(D) None of these
Solution:
$$ {0.042 \over 0.007}={0.42 \over 7}× 10={420 \over 7}=60 $$
LCM of Decimal Fraction
Step 1. Firstly make the same number of decimal places in all the given numbers.
Step 2. Find their LCM as if they were integers.
Step 3. Mark in the result as many decimal places as there are in each of the numbers.
Ex. Find the LCM of 0.80, 9.60, and 0.12.
(A) 9.6
(B) 0.96
(C) 0.096
(D) None of these
Solution:
The given numbers are equivalent to 0.80, 9.60 and 0.12.
Now, we will find the LCM of 80, 960 and 12.
LCM of 80, 960 and 12 = 960
![]() Required LCM of 0.80, 9.60 and 0.12 = 9.60
Required LCM of 0.80, 9.60 and 0.12 = 9.60
HCF of Decimal Fraction
Step I Firstly make the same number of decimal places in all the given numbers.
Step II Find their HCF as if they were integers.
Step III Mark in the result as many decimal places as there are in each of the numbers.
EX. Find the HCF of 15.5 and 0.90.
Solution:
The given numbers are equivalent to 1550 and 90. HCF of 1550 and 90.
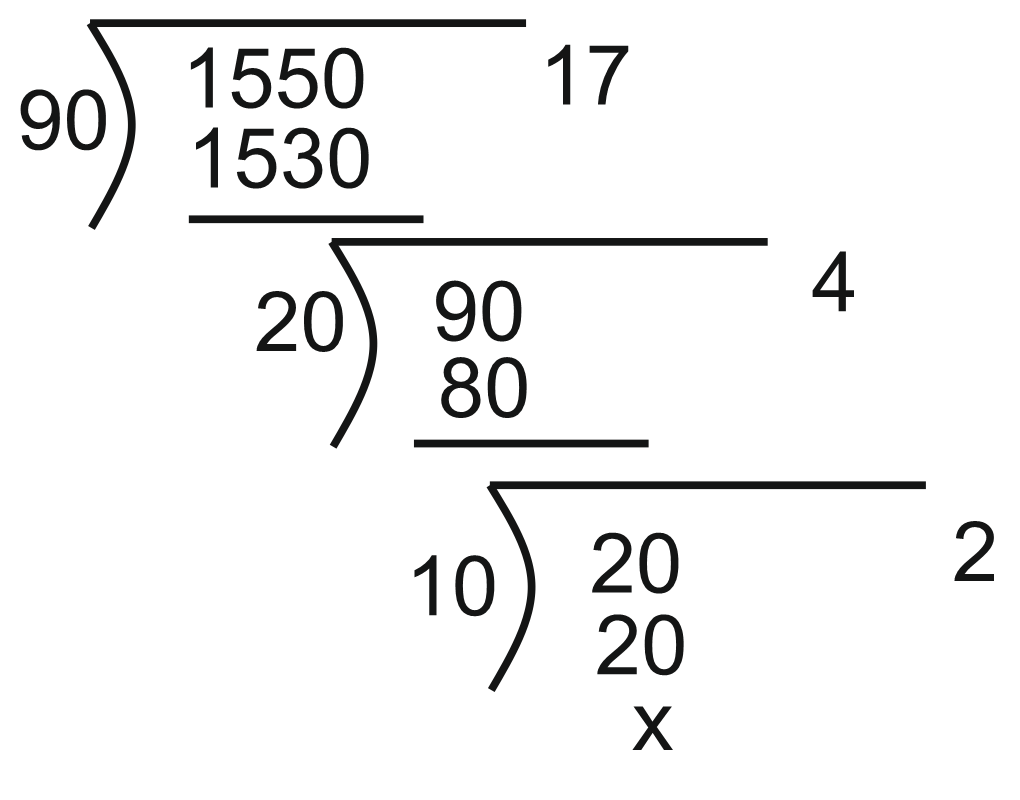
HCF of 1550 and 90 = 10
![]() HCF of 15.5 and 0.90 = 0.1
HCF of 15.5 and 0.90 = 0.1
These are the important decimal fraction formulas with examples which will help you in the competitive exams. Keep practice decimal fraction question-answers for your better score. Ask me in the comment section if you have any query related decimal fraction formula with exams for ssc or bank exams.



