Logarithmic Formulas and Equations with Examples for SSC and Bank Exams

Logarithm formulas are not difficult to use in aptitude questions. You just need to learn the correct way to use formulas and should know how many types of formulas you can use with logarithmic equations examples. 

With the help of this blog, you can easily learn how to use logarithmic formulas with different logarithm equations examples. These examples will help you using formulas in competitive exams. You can practice also logarithmic problems with solutions for your better performance.

Logarithmic Formulas and Equations Examples for Competitive Exams

Important facts and formulae

1. Logarithm: If a is a positive real number, other than 1 and a^m = x, then we write:

m=log_ax and we say that the value of log x to the base a is m.

Example :

(i) 10³=1000 → log₁₀ 1000 = 3

(ii) 3⁴=81 → log₃31 = 4

$$(iii) \ 2^{-3}={1\over8}→log_2{1\over8}=-3$$

(iv) (.1)²=.01 → log_(.1).01=2.

2. Properties of logarithms:

(i) log_a(xy)=log_ax+log_ay

(ii) log_a=log_ax-log_ay

(iii) log_xX=1

(iv) log_a1=0

(v) log_a(X^p)=p(log_aX)

$$(vi) \ log_ax={1\over log_ax}$$

$$(vii)\log_ax={log_bx\over log_ba}={logx\over loga} $$

Remember : When base is not mentioned, it is taken as 10.

3. Common Logarithms: Logarithms to the base 10 are known as common logarithms.

4. The logarithm of a number contains two parts, namely characteristic and mantissa.

Characteristic: The integral part of the logarithm of a number is called its characteristic.

Case I: When the number is greater than 1.

In this case, the characteristic is one less than the number of digits in the left of the decimal point in the given number.

Case II. When the number is less than 1.

In this case, the characteristic is one more than the number of zeros between the decimal point and the first significant digit of the number and it is negative.

Instead of -1, -2, etc. we write, 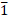(One bar) ,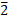(two bar), etc.

Example:

Number                Characteristic         Number         Characteristic    

348.25                              2                 0.6173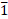                       

46.583                              1                 0.03125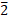                                       

9.2193                              0                 0.00125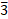                                 

Mantissa: The decimal part of the logarithm of a number is known is its mantissa for mantissa, we look through log table.

Solved examples 

Ex.1. Evaluate : (i) log₇ 1 = 0       (ii) log₃₄ 34          (iii) 36^log₆⁴

Solution 

(i) We know that log_a 1 = 0, so log₇ 1 = 0.

(ii) We know that log_a a = 1, so log₃₄ 34 = 0.

(iii) we know that a^log_a^x = x

Now, 36^log₆⁴ = (6²) ^log₆⁴ = 6^2(log₆⁴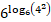⁾ = = 6^log₆¹⁶=16.

Ex.2. Find the value of x which satisfies the relation

log₁₀ 3+ log₁₀ (4x+1) = log₁₀ (x+1)+1

Solution 

log₁₀3+log₁₀(4x+1) = log₁₀(x+1)+1

⟺ log₁₀ 3 + log₁₀(4x+1)=log₁₀(x+1)+log₁₀10

⟺ log₁₀[3(4x+1)] = log₁₀[10(x+1)]

⟺ 3(4x+1) = 10(x+1) ⟺ 12x + 3 = 10x +10 ⟺ 2x = 7 ⟺ 

Ex.3. $$Simplifv =   \left({1\over log_{xy}(xyz)}+{1\over log_{yz}(xyz)}+{1\over log_{zx}(xyz)}\right)$$

Solution

Given expression = log_xyz(xy) + log_xyz(yz) +log_xyz(zx)

= log_xyz(xy × yz × zx) = log_xyz(xyz)²

  $$∴ \left(log_ax={1\over log_xa}\right)$$ = 2 log_xyz(xyz) = 2 × 1 = 2.

Ex.4. if log₁₀ 2 = 0.30103, Find the value of log₁₀50.

Solution

$$log_{10}50=log_{10}\left({100\over2}\right)=log_{10}100-log_{10}2 = 0.30103 = 1.69897$$

Ex.5. If log 2 = 0.30103, find the number of digit in 2⁵⁶

Solution 

Log(2⁵⁶)=56 log 2 = (56 × 0.30103) = 16.85768.

Its characteristic is 16. Hence, the number of digit in 2⁵⁶ is 17.

If you face any problem in these logarithmic formulas or want to ask anything regarding logarithmic equations examples and formulas, you ask me in the comment box. If you want to more practice of logarithm questions with answers visit here.