Problems on Trains Formulas and Sample Questions with Solutions

Hello students,

Problems on train formulas are important to solve the train problems quickly. In this blog, you can learn train problem formula and tricks to solve problems on trains. I have explained some problems on trains with solutions. Let’s learn together.

After learn or know problems on trains formulas and sample questions with solutions, you can practice with problems on trains aptitude questions and answers.

Problems on trains formula for quick solutions of train-based questions:

Remember some important formulas of train problems for instant solutions of problems on trains.

(1) x km/hr = 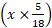 m/s.  m/s. 

(2) x m/s = 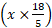 km/hr

3. Time taken by a train of length l metres to pass a pole or a standing man or a single post is equal to the time taken by the train to cover l metres

4. Time taken by a train of length l metres to pass a stationary object of length b metres is the time taken by the train to cover (l + b) metres.

5. Suppose two trains or two bodies are moving in the same direction at u m/s and v m/s, where u>v, then their relatives speed = (u - v) m/s.

6. Suppose two trains or two bodies are moving in opposite direction at u m/s and v m/s, then their relatives speed = (u + v) m/s.

7. If two trains of length a metres and b metres are moving in opposite directions at u m/s and v m/s, then time taken by the trains to cross each other =

8. If two trains of length a metres and b metres are moving in the same direction at u m /s and v m/ s, then the time take by the faster train to cross the slower train =

9. If two trains (or bodies) starts at the same time from points A and B towards each other and after crossing they take a and b sec in reaching B and A respectively, then (As speed): (B’s speed) = 

()

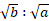Problem on trains with solutions – Train problems with solutions:

Let’s have some solved examples to understand the topic clearly.

Ex.1. A train 100 m long is running at the speed of 30 km/hr. find the time taken by in to pass a man standing near the railway line.

Solution:

Speed of the train = 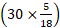m/sec = 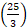m/sec.

Distance moved in passing the standing man = 100 m.

Required time taken = =sec = 12 sec.

Ex.2. A train is moving at a speed of 132 km/hr. If the length of the train is 110 metres, how long will it take to cross a railway platform 165 metre long?

Solution:

Speed of the train = 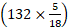m/sec. = 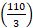m/sec.

Distance covered in passing the platform = (110+165) m = 275 m.

Time taken = 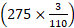sec =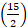 sec =7sec.

Ex.3 A man is standing on a railway bridge which is 180 m long. He finds that a train crosses the bridge in 20 seconds but himself in 8 seconds. Find the length of the train and its speed.

Solution:

Let the length of the train be x metres.

Then, the train covers x metres in 8 seconds and (x + 180) metres in 20 seconds.

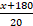   = ↔ 20 x = 8(x + 180) ↔ x = 120.

   Length of the train = 120 m.

Speed of the train = 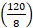m/sec = m/sec = 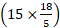kmph = 54 kmph.

Ex.4 A train 150 m long is running with a speed of 68 kmph. In what time will it pass a man who is running at 8 kmph in the same direction in which the train is going?

Solution:

Speed of the train relative to man = (68 – 8) kmph = 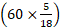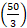m/sec = m/sec

Time taken by the train to cross the man = Time taken by it to cover 150 m at 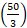 m/sec = 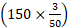sec = 9 sec.

Ex.5. A train 220 m long is running with a speed of 59 kmph. In what time will it pass a man who is running at 7 kmph in the direction opposite to that in which the train is going ?

Speed of the train relative to man = (59+7) kmph = 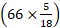 m/sec =  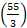m/sec.

Time taken by the train to cross the man = Time taken by it to cover 220 m at 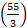 m/sec. =  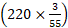sec = 12 sec.

Ex.6. Two trains 100 meters and 120 meters long are running in the same direction with speed of 72 km/hr and 54 km/hr. In how much time will the first train cross the second?

Solution 

Relative speed of the trains 

$$ = (72-54)\ km/hr = 18 \ km/hr$$

  $$=\left(18×{5\over2} \right)m /sec = 5\ m/ sec $$

Time taken by the trains to cross each other 

= Time taken to cover (100+120) m at 5 m/sec $$ = \left({220\over5} \right)sec=44sec$$

Ex.7. A train 100 metres long take 6 second to cross a man walking at 5 kmph in a direction opposite to that of the train. Find the speed of the train.

Solution 

Let the speed of the train be x kmph.

Speed of the train relative to man = (x+5) kmph $$(x+5)×{5\over18}\  m/sec.$$

  $$⸫ \ {100\over(x+5)×{5\over18}}=6↔30(x+5)=1800↔x=55.$$

⸫ Speed of the train is 55 kmph.

Ex.8. Two train 137 metres and 163 metres in length are running towards each other on parallel lines, one at the rate of 42 kmph and another at 48 kmph. In what time will they be clear of each from the moment they meet?

$$ Solution $$

$$ Relative \ speed \ of\ the \ trains \ = (42+48)\ kmph = 90\ kmph $$

$$= \left( 90 × {5\over18} \right)m/sec = 25 m/sec. $$

$$ Tiem \ taken\ by \ the \ trains \ to \ pass \ each \ other \ $$ $$= Time \ taken \ to \ (137+163)m \ at \ 25 \ m/sec = \left({300\over25} \right) sec = 12 \ sec$$

Ex.9. A train running at 54 kmph takes 20 seconds to pass a platform. Next it takes 12 seconds to pass a man walking at 6 kmph in the same direction in which the train is going. Find the length of the train and the length of the platform.

$$ Solution $$

Let the length of train be x metres and length of platform y metres.

Speed of the train relative to man = (54 – 5) kmph = 48 kmph.

$$= \left(40×{5\over18}\right)m/sec = {40\over3}m/sec  $$

In passing a man, the train covers its own length with relative speed.

$$ ∴  Length \ of \ train \ = (Relative×Time)= \left( {40\over3}×12 \right)m = 160 \ m $$

$$ Also, speed \ of \ the \ train \ = \left( 54× {5\over18} \right) \ m/sec = 15 \ m /sec. $$

$$ ∴ \ {x+y\over15}=20⟺ x+y = 300⟺ y= (300-160)\ m = 140 \ m  $$

Ex.10. A man sitting in a train which is travelling at 50 kmph observes that a goods trains, travelling in opposite direction, takes 9 seconds to pass him. If the goods trains is 280 m long, find its speed.

$$ Solution $$

$$ Relative \ Speed = \left({280\over9}\right)m / sec = \left({280\over9}×{18\over5}  \right)\ kmph = 112 \ kmph $$

  $$ ∴ \ Speed \ of \ goods\ train \ = (112 - 50) \ kmph = 62 \ kmph   $$

I hope you can solve train problems with the help of problems on trains formula and provided solved examples.

You can comment me if you face problems while solving problems on train.