Time Speed and Distance Questions for Competitive Exams

Time Speed and Distance is an important topic for those who are preparing for competitive exams. This topic is related to time, speed and distance. In this, you just need to know the time, speed and distance to reach any two-point (place).

Here in this blog, given time, speed and distance questions with solutions for your practice form which you can understand properly this topic. You should learn how to use formulas in time speed and distance questions. 

Questions of Time Speed and Distance

Q.1. A students walks from his house at 5/2 km/h and reaches his school late by 6 min. Next day, he increase his speed by 1 km/h and reaches 6 min before school time. How far is the school from his house?

(A) 5/4 km

(B) 7/4 km

(C) 9/4 km

(D) 11/4 km

Given, initial speed, a = 5/2.

And new speed, b= (5/2)+1 = 7/2.

Difference between two the times

= 6+6=12 min

According to the question,

X/(5/2) – X/(7/2) = 12/60→ 2X/5 – 2X/7 = 1/5

→14X-10X= 7 → X=7/4 km

Q.2. A thief is a spotted by a policeman from a distance of 200 m. When the policeman starts chasing, the thief also starts running. If the speed of the thief be 16 km/h and that of the policeman be 20 km/h, how far the thief will have run before he is overtaken?

(A) 800 m

(B) 850 m

(C) 700 m

(D) 650 m

= 16×(5/18) = 40/9 m/s.

And b = 20 km/h = 20×(5/18) = 50/9 m/s

Required distance = d×{a/(b-a)}

=

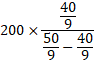
= 200×(40/10)=800m.

Q.3. A certain distance is covered at a certain speed. If half of this distance is covered in 4 times of the time, find the ratio of the two speed.

(A) 1:8

(B) 1:4

(C) 4:1

(D) 8:1

Then, First Speed = X/Y km/h

Again, X/2 km be covered in 4Y h.

New speed = (X/2)×(1/4Y)= X/8Y km/h

Hence, required ratio of speeds

= X/Y : X/8Y = 1: 1/8 = 8:1

Q.4. Sunil drives a motorcycle and covers a distance of 715 km at covered in 4 times of the time, find the ratio of the two speed.

(A) 65 km/h

(B) 55 km/h

(C) 60 km/h

(D) 36 km/h

→ 

→

→ x²+10= 

→ x²+65x – 55x – 3575 = 0

→ x (x – 55) (x+65) = 0

→ (x – 55)(x+65) = 0

→ x = 55 or x = - 65

Ignoring the negative value, we get X = 55

⸫ Original speed of the motorcycle = 55 km

Q.5. Amit walks at a uniform speed of 4 km/h and 4 h after his starts, Brijesh cycles after him at the uniform rate of 20 km/h. How far from the starting point will Brijesh catch Amit?

(A) 15 km

(B) 18 km

(C) 13 km

(D) 20 km

= Distance travelled by Brijesh in X h.

According to the question,

4(x+4) = 20x

→ (4x+16) = 20x

→ 16x = 16

→ x= 16/16=1

⸫ Distance travelled by Brijiesh in 1 h = 1 × 20 = 20 km

Q.6. A train leaves Manipur at 6 am and reaches Dispur at 10 am. Another train leaves Dispur at 8 am and reaches Manipur at 11:30 am. At what time do the two trains cross each other?

(A) 7 : 56 am

(B) 7 : 56 pm

(C) 8 : 56 am

(D) 8 : 56 pm

Average speed of train from Manipur = x/4 km/h

Let, they meet y h after 6 am.

Then, according to the question,

()+

→ (y/4)+2(y-2)/7=1

→ 7y+8(y-2)=28

→15y=44

→ y=(44/15)h= 2h 56 min

Clearly, trains meet 2 h 56 min after 6 am.

Hence, the train meet at 8 : 56 am.

Q.7. The distance between two stations X and Y is 450 km. A train L starts at 6 pm from X and Y is at average speed of 60 km/h. Another train M starts from Y at an average speed of 60 km/h. Another train M starts from Y at 5: 2 pm and moves towards x at an average speed of 80 km/h. How far from X will the two trains meet and at what time?

(A) 170 km, 8 : 50 pm

(B) 150 km, 7 : 50 pm

(C) 170 km, 6 : 50 pm

(D) 150 m, 9 : 50 pm

Then, (Time taken by M to cover

(450 – a) km) – (Time taken by L to cover a km) = 40/60.

→ (450-a)/80 – a/60 = 40/60.

→ (450-a)/80 = 40/60+a/60.

→ (450-a)/8 – (40+a)/6 = 0

→ 3(450-a) – 4(a+40)=0

→ 7a= 1190

→ a = 1190/7 = 170

⸫ Time  taken by L to cover 170 km = (170/60) h = 2 h 50 min.

Q.8. Two friends X and Y walk from A to B at distance of 39 km, at 3 km an hour and  km an hour respectively Y reaches B, returns immediately and meet X at C. Find the distance from A to C.

(A) 26 s

(B) 25 s

(C) 15 s

(D) 27 s

= 144 km/h

= 144×(5/18)m/s

= 8×5 = 40 m/s

Distance covered in passing each other = (512+528) m

= 1040 m

⸫ Required time = 1040/40 = 26s.

Q.9. A train passes two persons who are walking in the direction opposite to the direction of train at the rate of 10 m/s and 20 m/s respectively in 12s and 10s respectively. Find the length of the train.

(A) 500 m

(B) 900 m

(C) 400 m

(D) 600 m

a = 10 m/s and b = 20 m/s

Now, length of the train

= Difference in speeds × T1 × T2/ T1- T2

= (20-10)×12×10/12-10

= (10×12×10)/2

= 600 m.

Q.10. From stations M and N, two trains start moving towards each other at speed 125 km/h and 75 km/h respectively. When the two trains meet each 

(A) 190 km

(B) 200 km

(C) 145 km

(D) 225 km

Now, distance between the stations M and N

=

=

= (200/50)×50 = 200 km.

Ask me in the comment section if you face any problems regarding time speed and distance.