Compound Interest Problems with Solutions for SSC and Bank Exams

Compound interest problems asked in competitive exams usually. These compound interest problems are very important for SSC and Bank exams. So you must learn how to solve compound interest problems with solutions for ssc and bank exams.

Here in this blog, you can learn easily how to solve compound interest problems with examples and different-2 equations. You can learn using compound interest formulas with examples and brighten your performance level.

You should check solved examples so that you can easily understand how to use formulas while solving simple and compound interest questions.

Compound Interest Problems with Solutions for Competitive Exams

Q.1. Albert invested an amount of Rs. 8000 in a fixed deposit scheme for 2 years at compound interest rate 5 p.c.p.a. How much amount will Albert get on maturity of the fixed deposit?

(A) Rs. 8600

(B) Rs. 8620

(C) Rs. 8840

(D) None of these.

Solution:

$$ Amount \ = Rs\left(8000× {\left(1+{5\over100}\right)^2}\right)$$

   $$ =   \left(8000×{21\over20}×{21\over20}\right)=Rs.8820 $$

Q.2. What will be the compound interest on sum of Rs. 25,000 after 3 years at the rate of 12 p.c.p.a. ?

(A) Rs. 9000.30

(B) Rs. 9720

(C) Rs. 10123.20

(D) Rs. 10483.20

(E) None of these

Solution:

$$ Amount \ = Rs\left(25000× {\left(1+{12\over100}\right)^3}\right)$$

  $$ =   \left(25000×{28\over25}×{28\over25}×{28\over25}\right)=Rs.35123.20 $$

∴ C.I. = Rs. ( 35123.20 – 25000) = Rs. 10123.20

Q.3.The compound interest on Rs. 20,480 at  per annum for 2 years 73 days, is :

(A) Rs. 2929

(B) Rs. 3000

(C) Rs. 3131

(D) Rs. 3636

Solution:

  $$Time = 1\frac{2}{3} \ Years\ 2\frac{1}{5}Years$$

$$∴ Amount \ = Rs\left(20480× {\left(1+{25\over4×100}\right)^2}×{\left({1}+{{{1\over5}×{25\over4}}\over100}\right)}\right)$$

$$ =   \left(20480×{17\over16}×{17\over16}×{81\over80}\right)=Rs.23409. $$

∴ C.I. = Rs. (23480 -20480) = Rs. 2929.

Q.4. Sam invested Rs. 15,000 @ 10% per annum for one year. If the interest is compounded half-yearly, then the amount received by Sam at the end of year will be :

(A) Rs. 16,500

(B) Rs. 16,525.50

(C) Rs. 16,537.50

(D) Rs. 18,150

(E) None of these

Solution:

P = Rs. 15000; R = 10% p.a. = 5% per half – year; T = 1 year = 2 half – years.

$$∴ Amount \ = Rs\left(15000× {\left(1+{5\over100}\right)^2}\right)$$

$$=Rs{\left(15000+{21\over20}×{21\over20}\right)}= Rs.16537.50.$$ 

Q.5. If the simple interest on a sum of money for 2 years at 5% per annum is Rs. 50, what is the compound interest on the same at the same rate and for the same time ?

(A) Rs. 51.25

(B) Rs. 52.

(C) Rs. 54.25

(D)  Rs. 60

Solution:

$$∴ Sum = \left({50×100\over2×5}\right)=Rs.500$$

    $$∴ Amount \ = Rs\left(500× {\left(1+{5\over100}\right)^2}\right)$$

  $$ =   \left(500×{21\over20}×{21\over20}\right)=Rs.551.25 $$

∴ C.I. = Rs. (551.25 - 500) = Rs. 51.25.

Q.6. What will be the different between simple and compound interest @ 10% per annum on a sum of Rs. 1000 after 4 years ?

Solution:

(A) Rs. 31

(B) Rs. 32.10

(C) Rs. 40.40

(D) Rs. 64.10

(E) None of these

$$∴ S.I = Rs.\left({1000×10×4\over100}\right)=Rs.400$$

    $$∴ C.I \ = Rs\left(1000× {\left(1+{10\over100}\right)^4}-1000\right)=Rs.464.10.$$

∴  Difference = Rs. (464.10 – 400) = Rs. 64.10

Q.7. The difference between simple interest and compound interest on Rs. 1200 for one year at 10% per annum reckoned half-yearly is :

(A) Rs. 2.50

(B) Rs. 3

(C) Rs. 3.75

(D) Rs. 4

(E) None of these.

Solution:

$$∴ S.I = Rs.\left({1200×10×1\over100}\right)=Rs.120$$

    $$∴ C.I \ = Rs\left(1200× {\left(1+{5\over100}\right)^2}-1200\right)=Rs.123.$$

Q.8. The compound interest on Rs. 30,000 at 7% per annum is Rs. 4347. The period (in years) is: 

(A) 2

(B)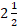

(C) 3

(D) 4

Solution:

Amount = Rs. (30000 + 4347) = Rs.34347.

Let the time be n years. Then,

$$3000 \left(1+{7\over100}\right)^n= 34347⟺\left({107\over100}\right)^n$$

   $$={34347\over30000}={11449\over10000}=\left({107\over100}\right)^2$$

  $$n = 2 \ Years$$

Q.9. At what rate of compound interest per annum will a sum of Rs. 1200 become Rs. 1348.32 in 2 years?

(A) 6%

(B) 6.5%

(C) 7%

(D) 7.5%

Solution:

$$1200 \left(1+{R\over100}\right)^2= 1348.32⟺\left(1+{R\over100}\right)^2$$

   $$={134832\over120000}={11236\over10000}$$

$$∴\left(1+{R\over100}\right)^2=\left({106\over100}\right)^2or \ 1+ {R\over100}={106\over100}or R=6 \% $$

Q.10. The compound interest on a sum of money for 2 years is Rs. 832 and the simple interest on the same sum for the same period is Rs. 800. The difference between the compound interest and the simple interest for 3 year will be :

(A) Rs. 48

(B) Rs. 66.56

(C) Rs. 98.56

(D) None of these.

 Deference in C.I and S.I for 2 years = Rs. 32. 

S.I. for one years = 400

S.I on Rs. 400 for one year = Rs. 32.

Hece difference in C.I and S.I for 3^rd year

$$= S.I = on Rs.   =   \left({832×8×1\over100}\right)=Rs. 66.56 $$

Total difference = (Rs. (32+66.56) = Rs. 66.56

I hope these examples are helpful to you. So, keep practice with these compound interest problems with solutions and you can practice compound interest questions and answers also. If you have any problem or doubt regarding compound interest problems with solutions, you can ask me in the comment section.