Simple and Compound Interest Formula for Competitive Exams

Compound interest and simple interest are important topics for ssc and banking students. In this blog, I am telling you about simple and compound interest formula. These formulas will help you to solve the questions in your exam.
Here are the solved examples with formulas so that you can easily understand how to use formulas while solving simple and compound interest questions. Click here for more practice Compound Interest Problems with Solutions and clear your doubts.
Formulas of Simple and Compound Interest
Practice with these questions and their examples below and improve your performance in the exam.
What are Simple interest and compound interest?
Interest:
When a person (borrower) takes money from another person or a bank (lender), then the first person pays some money to another person (lender) for the use of money lent. This extra money paid to the lander is known as interest.
Simple Interest:
The interest calculated uniformly only on the principle for the given time period is called the simple interest. It is nothing but the fix percentage of the principle (invested/borrowed money).
Principal (P) It is the sum of money deposited/loaned, also known as capital.
Interest (r) It is the extra money paid by borrower, calculated on the basis of principle for using the loan.
Time (T/n) The duration for which money is lent/borrowed.
Rate of Interest (r/R) It is the rate at which the interest is charged on principle.
Amount (A) Amount (A) = Principle (P) + Interest (r)
SI = 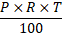
SI = ![]()
A = P + SI
P = 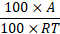
Where, SI = Simple Interest, P = Principle, R = Rate, T = Time and A = Amount.
Important -
● When time is given in days (D), covert it into year by dividing it by 365.
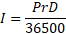
● Similarly, When the time is given in month (M), convert it into year by dividing it by 12.
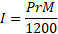
● A lent Rs. P1 to B for t1 yr and Rs. P2 to C for t2 yr received all together Rs s as interest
then r = ![]()
Compound Interest (CI)
While calculating compound interest which is calculated for the principle of first year, is added to the principle. The result of this addition becomes the principal for the next year. For this new principle, simple interest is calculated for second year and this interest is again added to the principal used for the second year. This new addition works as a principal for the third year and this process keeps going on for the stipulated time. Finally, the original principal is subtracted from the last year’s amount.
The result of this subtraction is called compound interest.
Let, Principle = P, Rate = R% per annum and Time = n yr
If interest is compounded annually, then
Amount = ![]()
Compound = 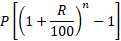
Or CI = Amount – Principle
If rates of interest are R1%, R2% and R3% for 1st yr, 2nd yr, and 3rd yr, respectively, then
Amount = ![]()
Important
● If interest is compounded half yearly, then
Amount =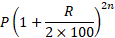
● If interest is compounded quarterly, then
Amount = 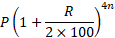
● If interest is compounded annually but time is in fraction (suppose, time = 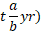 , then
, then
Amount = 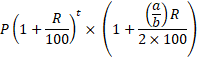
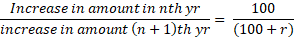
Similarly,
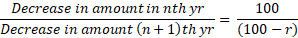
Where, r is rate of interest.
Example 1. A sum of money becomes four times in 20 yr at SI. Find the rate of interest.
(A) 10%
(B) 15%
(C) 25%
(D) 30%
If a sum of money becomes ‘n’ times ‘T’ yr at simple interest, then formula for calculation interest will be given as ![]()
Solution
Here, T = 20 yr, n = 4
⸫ ![]()
Example 2. The simple interest on Rs. 4000 in 3 yr at the rate of x% per annul equals to the simple interest on Rs. 5000 at the rate of 12% per annul in 2 yr. The value x is
(A) 6%
(B) 8%
(C) 9%
(D) 10%
Formula:
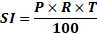
Hence, the two simple interest are equal,
Then, ![]()
Example 3. Simple interest on a certain sum is 16/25 of the sum. The rate percent, if the rate percent and time (in yr) are equal, is
(A) 6%
(B) 10%
(C) 8%
(D) 12%
Formula:
Simple interest = 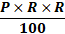
⸫ 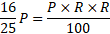
→ r2 = 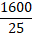
→ r = 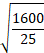
→ r = 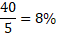
Example 4. If the simple interest for a certain sum for 2 yr at 5% per annul is Rs 200, what will be the compound interest for same sum for same period and at the same rate of interest?
(A) Rs 105
(B) Rs 110
(C) Rs 205
(D) Rs 200
Formula:
CI = ![]()
Given, SI = Rs 200, R = 5%
⸫ According to formula,
CI = ![]()
Example 5. There is 100% increase to an amount in 8 yr, at simple interest. Find the compound interest of Rs. 8000 after 2 yr at same rate of interest.
(A) Rs. 2500
(B) Rs. 2000
(C) Rs. 2250
(D) Rs. 2125
Formula
Compound = 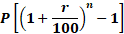
Let the rate of simple interest be r and principle x. According to the question, after 8 yr principle = 2x
Then, interest = 2x – x = x
![]()
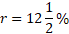
According to the case II, P = Rs. 8000
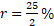 , , t = 2yr; A =
, , t = 2yr; A = ![]()
A = 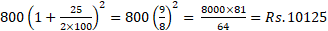
Compound interest = 10125-8000 = 2125.
Feel free and ask me anything in the comment section regarding simple and compound interest formula.



