Number System Questions and Answers with Solution

Welcome to our Number System Questions and Answers blog, your go-to resource for mastering the intricacies of number systems. Whether you're a student preparing for exams, a math enthusiast, or simply looking to enhance your mathematical skills, you'll find a wealth of valuable content here.
Number System Questions
Our Number System Questions and Answers blog features a wide range of number system questions, each accompanied by detailed solutions to ensure your complete understanding. We cover fundamental topics like integers, fractions, decimals, and real numbers, as well as more advanced concepts such as modular arithmetic and complex numbers.
Also, Read Latest Current Affairs Questions 2023: Current Affairs Today
"Stay ahead of the competition with our General Knowledge Mock Test and Current Affairs Mock Test!"
Number System Questions and Answers with Solution
Q : Which of the following fraction is the smallest? $$7\over 6 $$,$$7\over 9$$,$$4\over 5$$,$$5\over 7$$
(A) $$7\over 6 $$
(B) $$7\over 9$$
(C) $$4\over 5$$
(D) $$5\over 7$$
Correct Answer : D
Explanation :

The cube of 997 is
(A) 991026973
(B) 991029673
(C) 991029773
(D) 991027273
Correct Answer : A
Explanation :
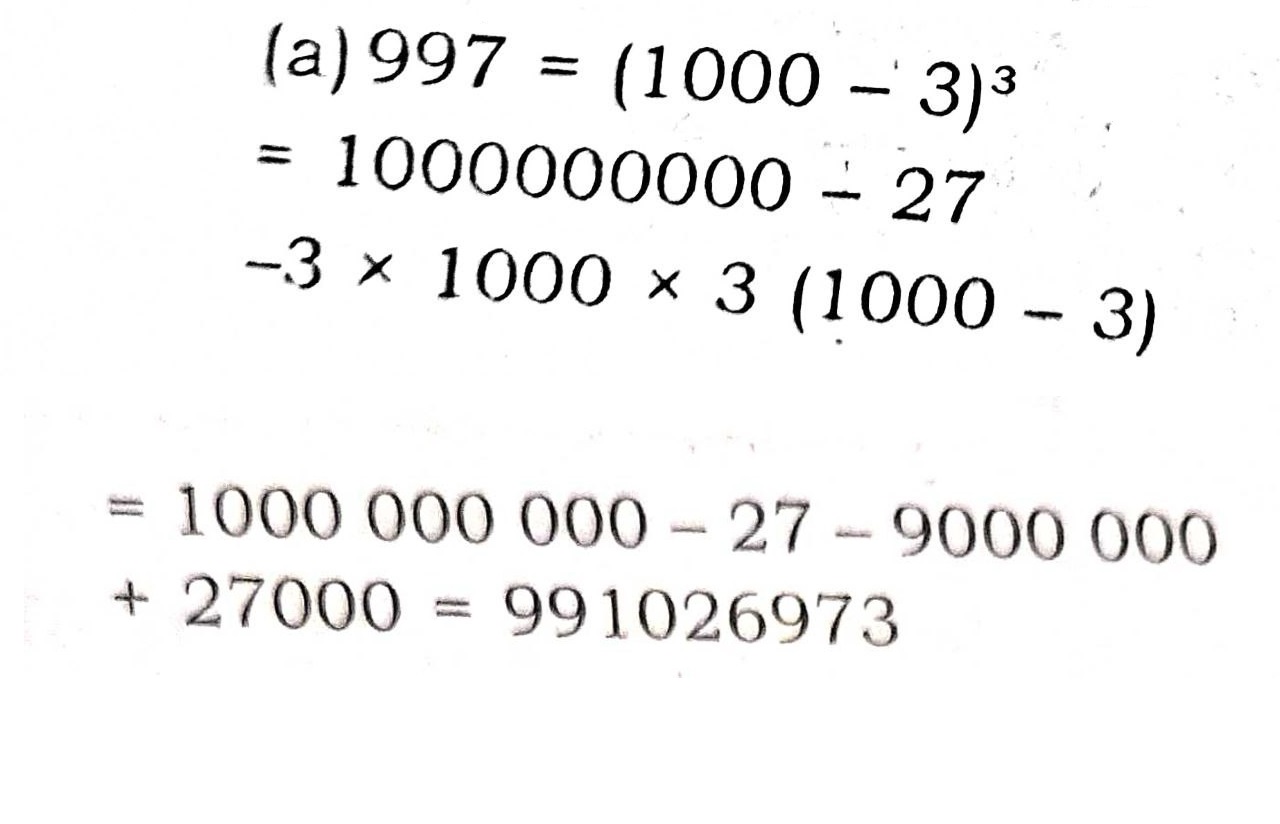
A number when divided by 899 gives a remainder 63. If the same number is divided by 29, the remainder will be
(A) 10
(B) 5
(C) 4
(D) 2
Correct Answer : B
Explanation :
Solution: $${Remainder\over 29}={7\over 9}$$
=> remainder (शेषफल)=5
96-11 when divided by 8 would leave a remainder of :
(A) 6
(B) 16
(C) 1
(D) 2
Correct Answer : A
Explanation :
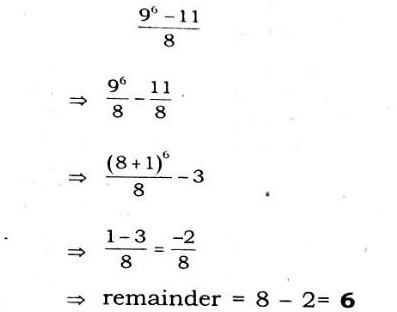
(49)15 – 1 is exactly divisible by:
(A) 29
(B) 8
(C) 50
(D) 51
Correct Answer : B
Explanation :

if 5432*7 is divisible by 9, then the digit in place of * is :
(A) 0
(B) 1
(C) 6
(D) 9
Correct Answer : C
Explanation :

Two positive numbers differ by 1280. When the greater number is divided by the smaller number, the quotient is 7 and the remainder is 50. The greater number is:
(A) 1558
(B) 1458
(C) 1585
(D) 1485
Correct Answer : D
Explanation :
Given :- Two positive numbers differ by 1280
When the greater number is divided by the smaller number The quotient is 7 and the remainder is 50
Concept :- Dividend = Quotient × divisor + remainder
Calculation :- Let greater number = a and Smaller number = b From question, ⇒ a - b = 1280 ....(1) Again from question, ⇒ a = 7b + 50 ....(2)
Put the value of a from equation (2) into equation (1) ⇒ 7b + 50 - b = 1280 ⇒ 6b = 1280 - 50 ⇒ 6b = 1230 ⇒ b = (1230/6) ⇒ b = 205
Put the value of b in equation (1) ⇒ a - 205 = 1280 ⇒ a = 1280 + 205 ⇒ a = 1485 ⇒ Greater number = 1485 ∴ Greater number is 1485
When 1062, 1134 and 1182 are divided by the greatest number .x, the remainder in each case is y. What is the value of (x − y)?
(A) 17
(B) 18
(C) 16
(D) 19
Correct Answer : B
Explanation :


The value of (x-y) will be 18
A number when divided by 296 gives a remainder 75. When the same number is divided by 37 the remainder will be:
(A) 8
(B) 1
(C) 2
(D) 11
Correct Answer : B
Explanation :
Let number (dividend) be X.
∴ X = 296 × Q + 75 where Q is the quotient and can have the values 1, 2, 3 etc.
= 37 × 8 × Q + 37 × 2 + 1
= 37 (8Q + 2) + 1
Thus we see that the remainder is 1.
[Remark : When the second divisor is a factor of the first divisor, the second remainder is obtained by dividing the first remainder by the second divisor.
Hence, divide 75 by 37, the remainder is 1].
A number when divided successively by 4 and 5 leaves remainder 1 and 4 respectively. When it is successively divided by 5 and 4 the respective remainders will be
(A) 2, 3
(B) 1, 2
(C) 4, 1
(D) 3, 2
Correct Answer : A
Explanation :
The least number X in this case will be determined as follows:
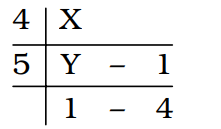
Y = 5 × 1 + 4 = 9
X = 4 × Y + 1 = 4 × 9 + 1 = 37 Now,
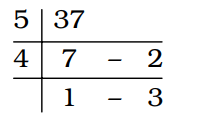
Hence, the respective remainders are 2, 3.



