Percentage Questions with Answers

Welcome to our 'Percentage Questions with Answers' blog, your go-to resource for mastering the art of percentages! Whether you're a student preparing for exams or someone looking to enhance their numerical skills, our Percentage Questions with Answers blog offers a comprehensive collection of percentage-related questions accompanied by detailed solutions. From basic concepts to advanced applications, we cover everything you need to confidently tackle percentage problems. Let's embark on this journey of numerical fluency together!
Percentage Questions
In this article Percentage Questions with Answers, we are sharing the most important Percentage Questions with Answers under the Aptitude section for those aspirants who are preparing for upcoming competitive exams.
Also, Read Latest Current Affairs Questions 2022: Current Affairs Today
Students can quickly get free General Knowledge Mock Test and Current Affairs Mock Test on this platform for online exam practice to obtain good marks in competitive exams.
Percentage Questions with Answers
Q : In an examination, 34% of the students failed in mathematics and 42% failed in English. If 20% of the students failed in both subjects, then find the percentage of students who passed in both subjects.
(A) 40%
(B) 41%
(C) 43%
(D) 44%
Correct Answer : D
Explanation :
To find the percentage of students who failed in at least one subject (A or B or both), we can use the principle of inclusion-exclusion:
Percentage of students who failed in at least one subject (A or B or both) = Percentage of students who failed in M + Percentage of students who failed in E - Percentage of students who failed in both subjects
= M + E - B
= 34% + 42% - 20% = 76% - 20% = 56%
So, 56% of the students failed in at least one subject.
Now, to find the percentage of students who passed in both subjects, we subtract the percentage of students who failed in at least one subject from 100%:
Percentage of students who passed in both subjects = 100% - Percentage of students who failed in at least one subject = 100% - 56% = 44%
Therefore, the percentage of students who passed in both subjects is 44%.
7,500 is borrowed at C.I. at the rate of 2% for the first year, 4% for the second year, and 5% for the third year. The amount to the paid after 3 years will be
(A) 8235.00
(B) 8432.00
(C) 8520.20
(D) 8353.80
Correct Answer : D
The cost price of a book is ₹110 and the selling price is ₹123.20. What percent profit will the bookseller make on selling it?
(A) 11%
(B) 12%
(C) 13%
(D) 14%
Correct Answer : B
Explanation :
To calculate the percentage profit made by the bookseller, we use the formula:
Profit Percentage=(Selling Price−Cost PriceCost Price)×100%Profit Percentage=(Cost PriceSelling Price−Cost Price)×100%
Given: Cost Price (𝐶𝑃CP) = ₹110
Selling Price (𝑆𝑃SP) = ₹123.20
Using the formula:
Profit Percentage=(123.20−110110)×100%Profit Percentage=(110123.20−110)×100%
Profit Percentage=(13.20110)×100%Profit Percentage=(11013.20)×100%
Profit Percentage=(0.12)×100%Profit Percentage=(0.12)×100%
Profit Percentage=12%Profit Percentage=12%
So, the bookseller will make a profit of 12%.
The sum of weights of A and B is 80 kg. 50% of A's weight is $${5\over6}$$ times the weight of B. Find the difference between their weights.
(A) 20 kg
(B) 10 kg
(C) 25 kg
(D) 15 kg
Correct Answer : A
Explanation :
Let's denote the weight of A as 𝑥x kg and the weight of B as 𝑦y kg.
Given:
- 𝑥+𝑦=80x+y=80 (Sum of weights of A and B is 80 kg)
- 0.5𝑥=56𝑦0.5x=65y (50% of A's weight is 5665 times the weight of B)
We can solve these two equations to find the values of 𝑥x and 𝑦y, and then calculate the difference between their weights.
From equation 2: 0.5𝑥=56𝑦0.5x=65y Multiply both sides by 2 to get rid of the fraction: 𝑥=56𝑦×2x=65y×2 𝑥=106𝑦x=610y 𝑥=53𝑦x=35y
Now substitute this expression for 𝑥x into equation 1: 53𝑦+𝑦=8035y+y=80 83𝑦=8038y=80 Multiply both sides by 3883: 𝑦=80×38y=80×83 𝑦=30y=30
Now that we have found the weight of B, we can find the weight of A using equation 1: 𝑥+30=80x+30=80 𝑥=80−30x=80−30 𝑥=50x=50
So, the weight of A is 50 kg and the weight of B is 30 kg.
Now, let's find the difference between their weights: Difference=Weight of A−Weight of BDifference=Weight of A−Weight of B Difference=50−30Difference=50−30 Difference=20Difference=20
Therefore, the difference between their weights is 20 kg.
The price of sugar increases by 15%. By what percentage should the consumption of sugar be decreased so that the expenditure on the purchase of sugar remains the same? [Give your answer correct to 2 decimal places.]
(A) 11.11%
(B) 12.5%
(C) 14.16%
(D) 13.04%
Correct Answer : D
Explanation :
To solve this problem, let's denote:
- Initial price of sugar = P
- Initial quantity consumed = Q
- Initial expenditure = PQ
After the price increases by 15%, the new price becomes 1.15P.
To keep the expenditure constant, the new quantity consumed (let's call it Q') can be calculated using the formula:
New expenditure = New price × New quantity
Setting the new expenditure equal to the initial expenditure:
PQ = (1.15P) * Q'
Now, solve for Q':
Q' = PQ / (1.15P)
Simplify:
Q' = Q / 1.15
Now, let's find the percentage decrease in consumption:
Percentage decrease = [(Q - Q') / Q] * 100
Substituting the value of Q':
Percentage decrease = [(Q - (Q / 1.15)) / Q] * 100
Percentage decrease = [(Q * (1 - 1/1.15)) / Q] * 100
Percentage decrease ≈ [(1 - 0.8696) * 100] ≈ 13.04%
Therefore, the consumption of sugar should be decreased by approximately 13.04% to keep the expenditure on the purchase of sugar the same after a 15% increase in price.
A is 150% of B and B is 40% of C. If A+B+C=20, then find the value of 2B+3C – 4A.
(A) 16
(B) 15
(C) 20
(D) 14
Correct Answer : D
Explanation :
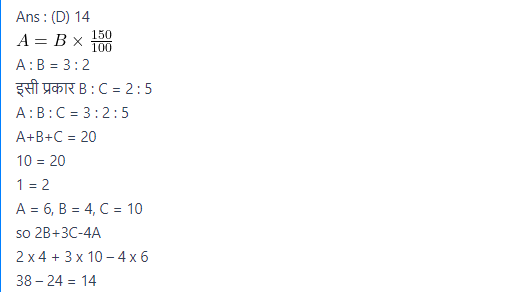
The population of a city increased by 15% in 2018 and 10% in 2019. Due to an epidemic, it decreased by 10% in 2020. Find the percentage increase in the population of the city in 3 years.
(A) 12.5%
(B) 17.5%
(C) 15%
(D) 13.85%
Correct Answer : D
Explanation :
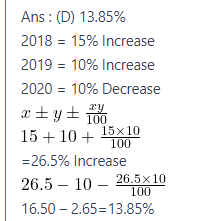
The income of A is 40% less than the income of B. If the income of A increases by 25% and the income of B increases by 40%, then the percentage increase in the combined income of A and B is ( Calculate up to two decimal places), will be ______.
(A) 37.86
(B) 31.67
(C) 35.19
(D) 34.38
Correct Answer : D
Explanation :
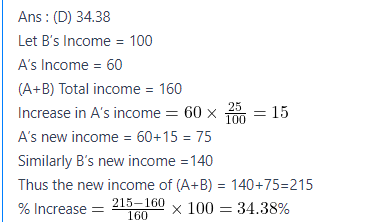
When the price of sugar is reduced by 20%, Sudhir gets 6 kg more sugar for Rs. 960. What is the reduced price of sugar per kg?
(A) 36
(B) 35
(C) 40
(D) 32
Correct Answer : D
Explanation :

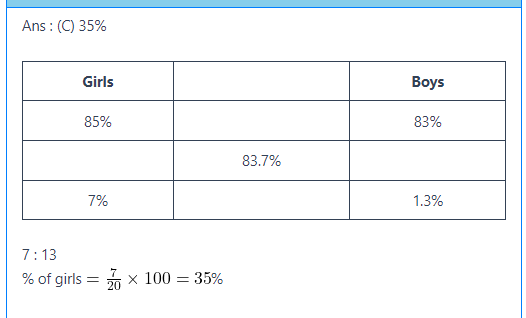
The average passing percentage of girls in the tenth class examination in a school is 85% and that of boys is 83%. The average passing percentage of all the boys and girls of the tenth class of that school is 83.7%. In the tenth class of that school Find the percentage of number of girls.
(A) 30%
(B) 40%
(C) 35%
(D) 45%
Correct Answer : C
Explanation :